Einsatzgebiete
Folgende Grafik zeigt einen kleinen Einblick, in welchen Bereichen Tabellenkalkulationssoftware verwendet wird. Vor allem aus dem kaufmännischen Bereich ist sie nicht mehr wegzudenken, wie ein Auszug aus den Anwendungsfeldern in der mittleren Spalte zeigt. Aber auch im wissenschaftlichen Bereich hat Tabellenkalkulation ihren Platz, insbesondere dann, wenn ein spezifischer Funktionsvorrat für Standardaufgaben aus den jeweiligen Bereichen angeboten wird (zB Statistikfunktionen, finanzmathematische Funktionen).
Abb. 1: Einsatzmöglichkeiten für Tabellenkalkulationsprogramme
Streifzug durch den Funktionsumfang
Dieser Funktionsvorrat ist in Tabellenkalkulationsprogrammen meist so umfangreich, dass er in Kategorien aufgeteilt wird. Da die reinen Grundrechnungsarten schon lange nicht mehr die Bedürfnisse der Anwender/innen abdecken, dürfen zusätzliche mathematische Formeln nicht fehlen. Dazu gehören sehr einfache Funktionen wie Summenbildung, Wurzelberechnungen, größter gemeinsamer Teiler und kleinstes gemeinsames Vielfaches, Restwert aus Divisionen (SUMME, WURZEL, GGT, KGV, REST ua), diverse Rundungsvarianten (RUNDEN, AUFRUNDEN, ABRUNDEN, VRUNDEN, GANZZAHL, KÜRZEN, GERADE, UNGERADE, OBERGRENZE, UNTERGRENZE ua) bis hin zu trigonometrischen und anderen typischen mathematischen Funktionen wie Logarithmen, Potenzberechnungen, Exponentialfunktionen, Fakultät und Zufallszahlen (SIN, ARCSIN, COS, ARCCOS, TAN, ARCTAN, COT, LN, LOG, LOG10, POTENZ, EXP, FAKULTÄT, ZUFALLSZAHL, ZUFALLSBEREICH, ua). Eine eigene Kategorie bildet meist die Finanzmathematik mit ihren typischen Zins- und Zinseszinsberechnungen in den verschiedensten Varianten, zB Berechnung von Effektiv- und Nominalverzinsung, Zinssätzen und Zinsbeträgen, Barwerten, Endwerten, Zahlungszeiträumen und regelmäßigen Zahlungen (EFFEKTIV, NOMINAL, ZINS,RENDITE, IKV, ZINSSATZ, BW, NBW, ZW, ZZR, RMZ ua) in Zusammenhang mit Kredit-, Zinsen-, Raten- und Wertpapierberechnungen.
Hinweis: Alle Funktionsangaben in diesem Abschnitt beziehen sich auf Libro Office Calc 5.0.5.2. Die Bezeichnungen, Kategorisierungen und der Funktionsumfang können bei anderen Produkten und Versionen abweichen.
Logische Funktionen liefern als Ergebnis WAHR oder FALSCH, oft auch mit 0 und 1 codiert. Ein häufig verwendeter Vertreter aus dieser Gruppe ist die WENN-Funktion, die es ermöglicht, abhängig von Bedingungen Ergebnisse anzuzeigen oder zu berechnen. Um mehrere Bedingungen zu prüfen, kann die
- WENN-Funktion mit
- UND sowie mit ODER kombiniert werden. Es gibt auch spezielle Funktionen in Verbindung mit WENN wie zB
- SUMMEWENN, (in Libre Office Calc in der Kategorie Mathematik zu finden)
- ZÄHLENWENN und MITTELWERTWENN (in Libre Office Calc in der Kategorie Statistik), die es ermöglichen, bestimmte Zellbereiche in die Bedingung einzuschließen.
Wissenschaftliche Anwendungsgebiete, die statistische Auswertungen erfordern, finden inzwischen in der Kategorie Statistik einen äußerst umfangreichen Funktionsvorrat, angefangen von einfachen Formeln für Anzahl, Rang, höchste, niedrigste und mittlere Werte
- ANZAHL, ANZAHL2, RANG, MAX, MIN, MITTELWERT, MODALWERT, MEDIAN, GEOMITTEL, HARMITTEL
bis hin zu Werten wie Standardabweichung, Varianz, Korrelationskoeffizient, Konfidenzintervall und diversen statistischen Tests
- NORMVERT, SCHIEFE, PHI, STABW, VARIANZ, KOVAR, KORREL, PEARSON, BESTIMMTHEITSMASS, KONFIDENZ, CHITEST, FTEST, GTEST, TTEST, ua.
In Libre Office Calc gibt es eine Kategorie Tabelle, die viele der Funktionen enthält, die in Excel in der Kategorie „Matrix“ enthalten sind. Diese Funktionen sind keine typischen Matrixfunktionen, da sie nur aus Zellbereichen nach bestimmten Vorschriften Werte zurückgeben, wie
- SVERWEIS, WVERWEIS, VERWEIS, INDEX, ZEILE, ZEILEN, SPALTE, SPALTEN.
Interessant ist auch die Funktion
- PIVOTDATENZUORDNEN, mit der Werte aus einer Pivottabelle übernommen werden können.
Im Gegensatz zu den klassischen Formeln bietet Tabellenkalkulation für gewöhnlich auch die Anwendung von Matrixformeln an. Erkennbar sind diese an den geschwungenen Klammern. Der entscheidende Unterschied besteht darin, dass Matrixformeln auf Zellbereiche ausgelegt sind. Dadurch sind der Input und/oder Output ganze Zellbereiche anstatt einzelner Zellen. Es gibt einige Funktionen, die direkt als Matrixformel ausgelegt sind zB
- HÄUFIGKEIT,
aber man kann Matrixfunktionen auch mit klassischen Formeln verknüpfen. Beispielsweise kann man mit {=WENN(A1:A3>1;“ja“;“nein“)} eine Wenn-Abfrage für 3 Zellen gleichzeitig gemacht werden. Bei Matrixformeln kann man im Nachhinein nie einen Teil des Ergebnisbereichs verändern. Das hat den Vorteil, dass die Einheitlichkeit der Formeln sichergestellt ist, kann im Einzelfall aber auch nachteilhaft sein. Oft kann mit Matrixformeln effizienter gearbeitet werden.
Versuchen Sie doch einmal Folgendes:
- Geben Sie in eine beliebige Zelle folgende Formel ein: =ZEILE(A1:A10)*SPALTE(A1:J1) und dann beenden Sie diese Formel mit str+shift+enter. Jetzt sollten 100 Zellen mit Ihnen vertraut erscheinenden Zahlenzusammenstellungen besetzt sein. Sie brauchen die geschwungene Klammer nie einzugeben, sie erscheint automatisch, wenn Sie die Funktion mit str+shift+enter abschließen und zeigt, dass es eine Matrixfunktion ist.
- Geben Sie folgende Funktion in eine Zelle außerhalb des A1:J10 ein, Abschluss wieder mit str+shift+enter, und erforschen Sie, was diese Funktion macht: =A1:J10
- Spannend wird es mit der folgenden Funktion, wenn Sie sie noch nicht kennen. Geben Sie sie wieder außerhalb des angegeben Bereichs ein. =MTRANS(A1:J10)
In Tabellenkalkulationsprogrammen findet man auch eine Kategorie Datenbank. Zu beachten ist hier allerdings, dass immer nur eine Tabelle (Relation, Datei) dargestellt und bearbeitet werden kann.
- DBANZAHL, DBMAX, DBMIN, DBMITTELWERT, DBSUMME, DBVARIANZ ua.
Funktionen sind keineswegs Zahlen vorbehalten, wie die zahlreichen Textfunktionen beweisen. Sie reichen von der Variation zwischen Groß- und Kleinschreibung, über das Finden, Ersetzen und Verändern von Textteilen, das Herausfinden von Merkmalen von Texten
- GROSS, GROSS2, KLEIN, KLEIN2, RECHTS, LINKS, TEIL, FINDEN, SUCHEN, ERSETZEN, VERKETTEN, SÄUBERN, GLÄTTEN, FEST, LÄNGE, IDENTISCH, ua
bis hin zu diversen Umformungsfunktionen
- BASIS, Dezimal, WERT, EUR, ARABISCH, RÖMISCH, ROT13, ua.
In der Kategorie „Add In“ in Libre Office Calc findet man weitere Umformungen, die in Excel in einer Kategorie „Technisch“ angeführt sind, wie zB Umformungen zwischen Binär-, Dezimal-, Hexadezimal- und Oktalzahlen
- BININDEZ, BININHEX, DEZINBIN, DEZINOKT, HEXINDEZ, usw.
Tabellenkalkulationsprogramme bieten umfangreiche Datums- und Zeitfunktionen an, da sie in der Lage sind, mit Datum und Uhrzeit zu rechnen. Grundlage dafür ist, dass jedes Datum und jede Uhrzeit als Zahl abgespeichert wird. Datumswerte sind immer ganze Zahlen, gezählt ab einem bestimmten Stichtag, und Uhrzeiten sind Nachkommastellen, also immer entsprechende Bruchteile eines Tages. Mit diesen Funktionen ist es nicht nur möglich, Rechenoperationen durchzuführen, sondern auch aktuelle Werte anzuzeigen und Teilinformationen aus einem Datum oder einer Uhrzeit herauszufiltern
- JAHRE,MONATE, TAGE, TAGE360, WOCHEN, DATUMDIF, EDATUM, HEUTE, JETZT, JAHR, MONAT, TAG, WOCHENTAG, KALENDERWOCHE, STUNDE, MINUTE, SEKUNDE, ua.
Schlussendlich sei hier noch die Kategorie Information erwähnt, die zahlreiche Möglichkeiten zur Abfrage von Zellinhalten oder Zusatzinformationen zu Zellen bietet. Alle Formeln, die mit IST beginnen, zB
- ISTZAHL, ISTFORMEL, ISTLEER,
liefern als Ergebnis WAHR oder FALSCH.
Dieser kurze Streifzug durch den Funktionsumfang von Tabellenkalkulationsprogrammen – der bei weitem nicht vollständig ist - macht deutlich, dass dieses Werkzeug sehr vielfältig einsetzbar ist. Gleichzeitig ist aber anzumerken, dass es keine Wundersoftware für alles ist. Obwohl mit Tabellenkalkulationsprogrammen sehr viele Aufgaben gelöst werden können, gibt es für die verschiedensten Einsatzbereiche Software-Werkzeuge, die speziell auf das entsprechende Thema zugeschnitten sind und daher bei Bedarf leistungsstärker sind.
Nehmen Sie an, Sie sollen für ein Seminar eine Fragebogenerhebung durchführen und statistisch auswerten. Sofern Sie nur wenige hundert Datensätze (oder unter hundert) auszuwerten haben und keine allzu großen Anforderungen an die zu ermittelnden statistischen Maße stellen, bietet ein Tabellenkalkulationsprogramm die Vorteile, dass es einfacher erlernbar/bedienbar ist, es kostenlose Versionen gibt und Sie es wahrscheinlich als Bestandteil von Office-Paketen verfügbar haben. Wenn Sie sich aber bereits gegen Ende Ihres Studiums befinden und sich für eine empirische Abschlussarbeit entschieden haben, dann reicht möglicherweise ein Tabellenkalkulationsprogramm nicht mehr aus oder wird in der Arbeit zu schwerfällig, und es könnte sinnvoll sein, eine speziell auf Statistik bzw. auf die von Ihnen benötigte Art von Statistik zugeschnittene Software (zB SPSS) ins Auge zu fassen.
So gibt es für verschiedenste Bereiche, in denen Tabellenkalkulationssoftware einsetzbar ist, Spezialprogramme für gehobene Ansprüche. Man kann zB in einem Tabellenkalkulationsprogramm längere Texte oder Briefe schreiben, besser geeignet dafür ist aber ein Textverarbeitungsprogramm. Abb. 1 oben wurde zB mit Libre Office Calc erstellt, könnte aber genauso gut oder sogar besser mit einem Textverarbeitungsprogramm umgesetzt werden. Trotz vieler mathematischer Funktionen könnte für spezielle mathematische Aufgaben GeoGebra, Sage, etc. angebrachter sein, für die Implementierung einer umfassenden Kostenrechnung mögen spezielle branchenspezifische Softwareprodukte über einen geeigneteren Funktionsumfang verfügen oder eine umfangreiche ERP-Software mehrere betriebliche Anforderungen abdecken. Im Bereich Datenbanken ist schnell ersichtlich, dass komplexere Aufgaben Datenbankprogramme mit einen adäquaten Funktionsvorrat benötigen.
Ein mächtiges Tool gibt es noch in Tabellenkalkulationsprogrammen, das es erlaubt, zusätzliche Ansprüche zu realisieren, nämlich Makros. Allerdings kommt man dabei sehr schnell tiefer ins Programmieren und für ungeübte Benutzer ist es schwierig und zeitaufwändig.
Daneben gibt es noch eine Reihe zusätzlicher Anwendungsmöglichkeiten, die viele Arbeiten in der kaufmännischen und wissenschaftlichen Praxis unterstützen und vereinfachen wie zB Pivottabellen, Konsolidieren von Tabellen, Zielwertsuche, Was-wäre-wenn-Analyse, Solver oder einfach nur die Möglichkeiten, Eingaben abzuprüfen und zu kommentieren. Einige dieser Anwendungsmöglichkeiten werden im Kapitel „Ausgewählte Funktionen am Beispiel von Libre Office Calc genauer vorgestellt.
Charts (Diagramme)
Ein wesentliches Einsatzgebiet von Tabellenkalkulationsprogrammen sind die üblicherweise integrierten Möglichkeiten, Daten auch grafisch darzustellen in Form von diversen Diagrammen (Charts). Diese Diagrammfunktionen sind inzwischen so gut ausgereift, dass es sogar sinnvoll sein kann, nur Daten aus anderen Programmen (zB Datenbankprogrammen) zu importieren, um sie in einem Tabellenkalkulationsprogramm grafisch aufzubereiten. Der Vorteil von Diagrammen ist im Vergleich mit dem zugrundeliegenden Datenmaterial offensichtlich: Visuelle Darstellungen sind für den Menschen leichter und schneller erfassbar.
Bei der Gestaltung eines Charts ist zu berücksichtigen, für welche Zwecke es verwendet werden soll. Soll das Diagramm als Ausdruck in schriftlicher Form weitergegeben werden (zB in einem Buch, Skript, Arbeitsunterlage), so ist darauf zu achten, dass alle nötigen Beschriftungen (Überschrift, Achsen, Maßeinheiten, etc) enthalten sind. Für die Verwendung eines Diagramms in einer Präsentation dagegen müssen verwendete Texte auch lesbar sein(Schriftgröße!), durch die Farbwahl ein angemessener Kontrast entstehen und die Zuhörer sollen nicht durch zu viele Nebensächlichkeiten abgelenkt werden. Da während einer Präsentation zum Chart gesprochen wird, ist es nicht notwendig, alle Elemente zu beschriften, im Gegenteil, man kann sogar bewusst auf einzelne Informationen verzichten, um Neugier zu wecken und dann im Vortrag darauf einzugehen.
Für fast alle Diagrammarten ist eine 3D-Version verfügbar. In manchen Fällen wirkt ein 3D-Effekt für das Auge angenehmer, in anderen Fällen – häufig bei sehr umfangreichem Datenmaterial – kann er störend wirken.
Da inzwischen eine breite Palette von Charts verfügbar ist, stellt sich die Frage, welches Diagramm für welche Daten bzw. für welche Aussagedimension am besten geeignet ist. Daher sollen hier die wichtigsten Diagrammtypen und ihre vorrangigen Einsatzbereiche kurz dargestellt werden.
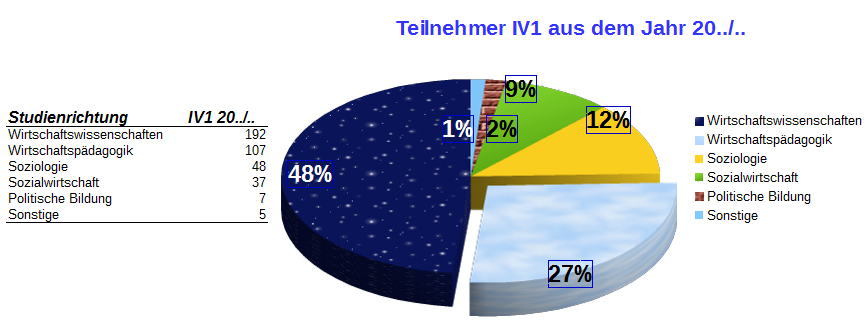
Kreisdiagramm: Es eignet sich besonders zur Darstellung von Anteilen an einem Ganzen (100%). Einzelne Kreissegmente können nicht nur durch diverse Formatierungen hervorgehoben werden, sondern auch durch Herausschieben von Kreissegmenten. Die Reihenfolge der einzelnen Anteile ist hier nicht von Bedeutung (um eine solche darzustellen, ist ein Säulen- oder Balkendiagramm zu wählen), allerdings ist zu beachten, dass nicht zu viele „Anteile am Kuchen“ in die Grafik umgesetzt werden, da sonst das Kreisdiagramm schnell unübersichtlich wird. Empfehlenswert sind maximal 10 Anteile; soll unbedingt mehr dargestellt werden, besteht die Möglichkeit, manche Anteile in Gruppen zusammenzufassen, um zu einer übersichtlichen Darstellung zu kommen.
Abb. 2: Kreisdiagramm
Säulen- und Balkendiagramm: Sehr häufig zum Einsatz kommt das Säulendiagramm, da es vielseitig verwendbar ist. Traditionell wird die waagrechte Achse als Zeitachse verwendet und ermöglicht die Darstellung von Entwicklungen. Die einzelnen Säulen werden trotzdem als voneinander unabhängige Elemente wahrgenommen (zB die Umsatzentwicklung über mehrere Jahre). Im Unterschied zu Kreisdiagrammen, können damit mehrere Datenreihen dargestellt werden. Ein wesentlicher Faktor für die Darstellung der Größenverhältnisse ist die verwendete Skalierung. Diese sollte für eine Diagrammreihe mit ähnlichen Inhalten gleich gehalten werden, da ansonsten leicht ein falscher Eindruck beim Betrachter entsteht. Allein schon, wenn man die die Höchstwerte variiert, entsteht optisch ein anderer Eindruck über Größenverhältnisse. Bedenklich ist, dass Skalierungswechsel auch ganz bewusst eingesetzt werden, um für die Betrachter gewünschte Effekte unangemessen zu betonen.
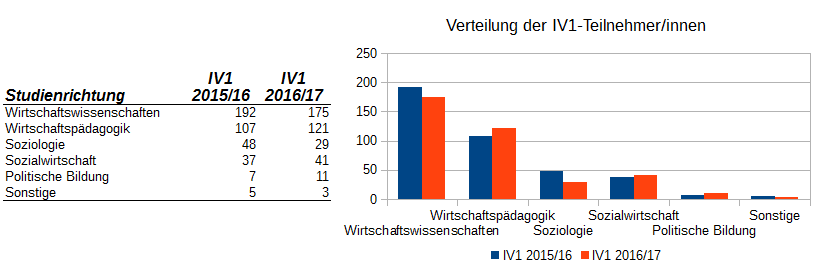
Abb. 3 zeigt wieder die Verteilung von IV1-Teilnehmer/innen, diesmal aus zwei Jahren. Es handelt sich hier um ein standardmäßig in Libre Office Calc aus den angezeigten Daten erzeugtes Chart, ohne Änderungen. Es ist zu erkennen, dass die Texte für die Studienrichtungen zu lange für die Grafik sind und daher mehrzeilig angezeigt werden. Man könnte nun diese Texte senkrecht oder schräg stellen, wodurch aber Lesbarkeit und Gesamtbild stark beeinträchtigt würden. Eine Abhilfe bieten hier Balkendiagramme.
Abb. 3: Säulendiagramm
Balkendiagramme sind im Prinzip das Gleiche wie Säulendiagramme, nur dass die Rubriken- und Größenachse vertauscht sind. Prinzipiell sind sie austauschbar. Beachten sollte man, dass Zeitfolgen üblicherweise auf der Rubrikenachse erwartet werden. Sehr gut eignet sich ein Balkendiagramm, wenn qualitative Merkmale dargestellt werden sollen, insbesondere, wenn es sich um längere Texte handelt. Texte bleiben so leichter lesbar ohne die grafische Darstellung zu behindern. Wenn kein anderes Ordnungskriterium sinnvoll erscheint, sollte nach Größen sortiert werden.
Abb. 4: Balkendiagramm
Hier wurde zusätzlich eine Achsenbezeichnung für die Rubrikenachse eingefügt. Vor allem, wenn Charts selbsterklärend sein sollen, ist besonders darauf zu achten.
Beide Diagrammtypen bieten die Möglichkeit, Säulen – bzw. Balken – zu stapeln. Das ist sinnvoll, wenn die Gesamtheit der einzelnen Teile etwas bedeutet. Eine weitere Darstellungsmöglichkeit besteht darin, alle Einzelwerte in Prozentanteile von 100 umzurechnen. Damit kann man wie beim Kreisdiagramm die Anteile vom Gesamten darstellen, allerdings nicht nur für eine Ausprägung (zB ein Jahr), sondern in einem Diagramm für Ausprägungen.
Ringdiagramm: Auch damit können mehrere Datenreihen dargestellt werden. Abb. Xx wurde aus dem gleichen Datenmaterial erstellt, nur wurde das spätere Jahr vorne hingestellt, da die aktuelleren – oder auch wichtigeren – Daten möglichst im äußeren Ring dargestellt werden sollen. Für die Datenbeschriftung wurden hier absolute Zahlen gewählt, es wäre ebenso wie im Kreisdiagramm in Abb. Xx eine Prozentdarstellung ansprechend.
Abb. 5: Ringdiagramm
Linien- und Flächendiagramm: Der Vorteil von Liniendiagrammen im Vergleich zu Säulendiagrammen besteht darin, dass eine viel größere Anzahl von Daten dargestellt werden kann, wobei die einzelnen Datenpunkte nicht so stark hervorgehoben sind. Durch die Verbindung der Datenpunkte mit einer Linie gewinnt der Betrachter den Eindruck, dass auf der gesamten Linie Datenpunkte vorhanden sind, obwohl dem nicht so ist. Daher ist diese Form der Darstellung nur zu empfehlen, wenn dieser Eindruck auch gerechtfertigt ist. Die Rubrikenachse muss auf jeden Fall einen größenmäßigen Verlauf darstellen (zB zeitlich), qualitative Merkmale wie in Abb. Xx sind in einem Liniendiagramm auf der Rubrikenachse nicht sinnvoll.
Abb. 6: Liniendiagramm
Auch dieses Diagramm wurde automatisch aus den vorgegebenen Daten erzeugt. Da auch hier zu wenig Platz in der Rubrikenachse zur Verfügung stand, wurde der Text automatisch schräg gestellt und jeweils ein Tag ausgelassen. Die Software versucht, einen geeigneten Anzeigemodus zu wählen, dieser kann natürlich nach Bedarf später abgeändert werden.
Ähnlich dem Liniendiagramm sind Flächendiagramme, hier sind allerdings die Flächen zwischen den Linien farbig ausgefüllt. Dieses Diagramm ist zu empfehlen, wenn nicht so sehr die Linie als Entwicklung, sondern die darunter liegend Fläche als Größenverhältnis ins Auge fallen soll.
Kursdiagramm: Eine neuere Form von Charts bietet die Möglichkeit, Höchst- und Tiefstwerte gemeinsam mit mittleren Werten in Beziehung zu setzen und darzustellen. Erweiterte Möglichkeiten beziehen zusätzliche Datenreihen mit ein. Wie der Name des Diagramms schon ausdrückt, eignet es sich insbesondere zur Darstellung von Kursentwicklungen an der Börse. In Abb. Xx ist ersichtlich, dass waagrecht der mittlere Wert dargestellt ist und die senkrechte Linie vom höchsten zum niedrigsten Wert zeigt.
Abb. 7: Kursdiagramm
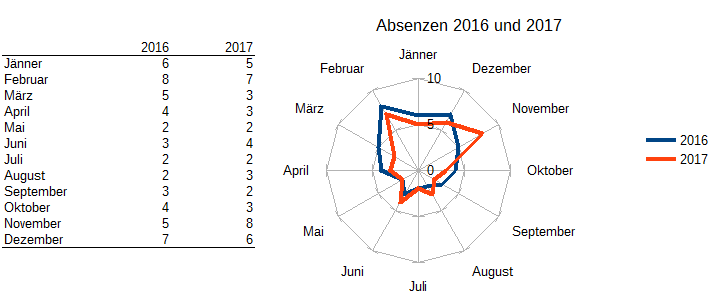
Netzdiagramm: Es eignet sich zur Darstellung von zyklischen Prozessen oder Daten wie zB Temperaturen oder Niederschlagsmengen im Verlauf einer bestimmten Zeiteinheit oder Wachstumszyklen. In Abb. Xx sind durchschnittliche Abwesenheiten pro Person in Tagen über das Jahr verteilt dargestellt. Wie man sieht, können auch mehrere Datenreihen dargestellt werden, bei mehr als zwei oder drei Datenreihen wird das Chart schnell unübersichtlich.
Abb. 8: Netzdiagramm
Xy-Diagramm und Blasendiagramm: Es eignet sich, wenn zwei numerische Achsen vorhanden sind, die zueinander in einer rechnerischen Beziehung stehen. Darunter fallen alle typischen Darstellungen von Funktionen im Koordatensystem. Äußerlich gleicht dieses Diagramm dem Liniendiagramm, der Unterschied liegt in der zweiten numerischen Achse. Als Beispiel sei hier eine typische Funktion aus dem Bereich der Betriebswirtschaftslehre dargestellt: Gegeben sind fixe und variable Kosten sowie der Verkaufspreis. Daraus wurden der Erlös und die Kosten bei gegebenem Absatz berechnet und als Diagramm dargestellt.
Abb. 9: Xy-Diagramm
Blasendiagramme verwenden drei numerische Datenreihen, die voneinander unabhängig sein dürfen. Eine davon wird auf der x-Achse, eine auf der y-Achse und die dritte durch die Größe der Blasen dargestellt. Bei der Erstellung ist auf die richtige Zuordnung der Datenreihen zu den Achsen zu achten. Die Anzahl der Datenpunkte sollte relativ klein sein, weil das Diagramm sonst schnell unübersichtlich wird. Eine typische Anwendung sind Marktwachstums-/Marktanteils-Portfoliodiagramme, die die erwähnten Größen von verschiedenen Produkten auf der x- und y-Achse darstellen und den Umsatz durch die Blasengröße. Abbildung 10 zeigt ein anderes Beispiel, hier werden die Marktanteile durch die Blasengröße symbolisiert.
Abb. 10: Blasendiagramm
In Abbildung 10 werden die Seminarbezeichnungen als Datenbeschriftung angezeigt, der Prozentsatz für den Marktanteil ist nicht ablesbar, könnte aber über die Blasenbeschriftung leicht hinzugefügt werden.
Literatur
Quellen:
Vonhoegen Helmut, Excel 2016, 1. Auflage, Bonn 2016
Zitiervorschlag
Höller-Furtlehner in Höller, Informationsverarbeitung, Tabellenkalkulation - Einsatzgebiete (mussswiki.idb.edu/ivwiki)