Kryptographie: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Admin (Diskussion | Beiträge) K Textersetzung - „mussswiki.idv.edu“ durch „mussswiki.idb.edu“ |
||
| (27 dazwischenliegende Versionen von 7 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
<yambe:breadcrumb>Sicherheit|Sicherheit</yambe:breadcrumb> | <!--<yambe:breadcrumb>Sicherheit|Sicherheit</yambe:breadcrumb>--> | ||
{{Kurzform|Die | {{Kurzform|Die Kryptographie verhalf über Tausende von Jahren hinweg dem Wunsch, Nachrichten nur an die berechtigten (gemeinten) Empfänger geraten zu lassen, zur teilweisen Erfüllung. Die heute vorherrschende Computerkryptographie will noch immer dasselbe und einiges darüber hinaus.}} | ||
| Zeile 10: | Zeile 10: | ||
Der Begriff "Chiffre" stammt aus dem Arabischen (sifr) und bedeutet soviel wie "nichts". Chiffren waren bereits in der griechischen und römischen Kultur von großer Bedeutung. In der europäischen Kultur wurden Chiffren im Mittelalter von Geheimbünden, weltlichen und kirchlichen Autoritäten benutzt und sind in zahlreichen Formen und Anwendungen bekannt bzw. erhalten. | Der Begriff "Chiffre" stammt aus dem Arabischen (sifr) und bedeutet soviel wie "nichts". Chiffren waren bereits in der griechischen und römischen Kultur von großer Bedeutung. In der europäischen Kultur wurden Chiffren im Mittelalter von Geheimbünden, weltlichen und kirchlichen Autoritäten benutzt und sind in zahlreichen Formen und Anwendungen bekannt bzw. erhalten. | ||
Während Chiffren mit dem Ersetzen (Substitution) und Vertauschen (Transposition) von Buchstaben und singulären Zeichen arbeiten, verwenden Codes ganze Wörter bzw. Begriffe. Der Einsatz der Chiffren erwies sich jedoch als flexibler und im Zusammenhang mit der Anwendung von Computerprogrammen vielseitig anwendbar, sodass die heutige Anwendung der Kryptographie als Weiterentwicklung der Methoden des Chiffrierens angesehen werden kann. | Während Chiffren mit dem Ersetzen (Substitution) und Vertauschen (Transposition) von Buchstaben und singulären Zeichen arbeiten, verwenden Codes ganze Wörter bzw. Begriffe. Der Einsatz der Chiffren erwies sich jedoch als flexibler und ist im Zusammenhang mit der Anwendung von Computerprogrammen vielseitig anwendbar, sodass die heutige Anwendung der Kryptographie als Weiterentwicklung der Methoden des Chiffrierens angesehen werden kann. | ||
== Begriffe == | == Begriffe == | ||
Die unverschlüsselte Botschaft wird allgemein als '''Klartext''', der Vorgang des Verschlüsselns | Die unverschlüsselte Botschaft wird allgemein als '''Klartext''', der Vorgang des Verschlüsselns als '''Chiffrieren''' und das Ergebnis der Verschlüsselung als '''Geheimtext oder Kryptogramm''' bezeichnet. Das Rückführen des Klartextes aus dem Kryptogramm nennt sich '''Dechiffrieren'''. Die Verallgemeinerung des Chiffrierens wird als '''Kryptographie''' bezeichnet. | ||
In formaler Schreibweise wird das soeben Beschriebene wie folgt dargestellt: | In formaler Schreibweise wird das soeben Beschriebene wie folgt dargestellt: | ||
| Zeile 22: | Zeile 22: | ||
klar = DECHIFF (krypt) | klar = DECHIFF (krypt) | ||
Der Klartext "klar" wird mit der Methode "CHIFF" in den Geheimtext "krypt" verwandelt. Der Geheimtext "krypt" wird mit der Methode | Der Klartext "klar" wird mit der Methode "CHIFF" in den Geheimtext "krypt" verwandelt. Der Geheimtext "krypt" wird mit der Methode "DECHIFF" wieder in den Klartext "klar" rückverwandelt. | ||
Der systematische Versuch, den Klartext ohne Kenntnis der Methode und der Schlüssel | Der systematische Versuch, den Klartext ohne Kenntnis der Methode und der Schlüssel rückzuverwandeln, heißt '''Kryptoanalyse'''. | ||
Das Ziel des Chiffrierens war Jahrhunderte lang dasselbe: Es galt zu verhindern, dass Unberechtigte in Kenntnis von geheimen Botschaften kamen. Heute, im Zeitalter der globalen Vernetzung, sind die Zielsetzungen und Anwendungsgebiete der modernen Kryptographie vielfältiger. | |||
== Transposition und Substitution == | == Transposition und Substitution == | ||
Zwei Methoden beherrschen die Chiffrierung | Zwei Methoden beherrschen die Chiffrierung: das Vertauschen der Zeichen des Klartextes, die '''Transposition''', und das Ersetzen des Klartextalphabetes durch ein Chiffrenalphabet, die '''Substitution'''. Das Prinzip der Substitution kann als allgemein bekannt angenommen werden, denn es wurden und werden Geheimalphabete bereits in jungen Jahren gerne eingesetzt. Ein einfaches Transpositionsbeispiel findet sich aus vorchristlicher Zeit, die Skytale. | ||
[[Datei:skyate.gif]] | [[Datei:skyate.gif]] | ||
| Zeile 45: | Zeile 44: | ||
[[Datei:Rosenkreuzer_alphabet.gif]] | [[Datei:Rosenkreuzer_alphabet.gif]] | ||
Die lateinische Bezeichnung für Rosenkreuzer "Rosicrucians", nach der Rosenkreuzer-Schablone chiffriert, ergibt in Anwendung der Rosenkreuzer-Schablone folgende Chiffre: | |||
[[Datei:Rosicrucians.gif]] | [[Datei:Rosicrucians.gif]] | ||
Neben den Lücken in der Geheimhaltung der Methode | Neben den Lücken in der Geheimhaltung der Methode ist aus heutiger Sicht die Tatsache, dass die Häufigkeit und die Verteilung der Buchstaben eines Alphabets lebender Sprachen nicht gleichwahrscheinlich ist, größter Schwachpunkt monoalphabetischer Substitution. Die Tatsache der statistischen Häufungen bestimmter (Bit-)Muster wird aber als Positivum in der Datenkompression genutzt. | ||
Mit der Leistungsfähigkeit heutiger Personalcomputer wären die meisten Kryptogramme mit monoalphabetischer Substitution in wenigen Sekunden entschlüsselt. | |||
== Polyalphabetische Substitution == | == Polyalphabetische Substitution == | ||
Die Tatsache der leichten Knackbarkeit monoalphabetischer | Die Tatsache der leichten Knackbarkeit monoalphabetischer Substitution führte bereit im 15. Jahrhundert zur polyalphabetischen Substitution. Dabei wird das Geheimtextalphabet während der Verschlüsselung öfter gewechselt. Je öfter, um so sicherer war und ist die Methode. | ||
Am einfachsten ist die polyalphabetische Substitution anhand der Chiffrierscheibe des italienischen Architekten Leon Battista Alberti darstellbar. | Am einfachsten ist die polyalphabetische Substitution anhand der Chiffrierscheibe des italienischen Architekten Leon Battista Alberti darstellbar. | ||
| Zeile 63: | Zeile 61: | ||
[[Datei:Albertis_scheibe.gif]] | [[Datei:Albertis_scheibe.gif]] | ||
Alberti konstruierte zwei Scheiben, die zueinander verdrehbar sind. Die äußere Scheibe enthält das Klartextalphabet, die innere das Chiffrenalphabet, der Vorgang des Chiffrierens erfolgt durch die Abbildung der Entsprechung von | Alberti konstruierte zwei Scheiben, die zueinander verdrehbar sind. Die äußere Scheibe enthält das Klartextalphabet, die innere das Chiffrenalphabet, der Vorgang des Chiffrierens erfolgt durch die Abbildung der Entsprechung von außen nach innen. Die Sicherheit dieser Methode besteht nun darin, dass die Stellung der beiden Scheiben zueinander während der Chiffrierung gewechselt wird. Jede unterschiedliche Stellung der Scheiben zueinander entspricht einem neuen Alphabet. Jede Folge von Stellungswechseln ebenfalls. | ||
Eine Anweisung zum Dechiffrieren könnte beispielsweise lauten: | Eine Anweisung zum Dechiffrieren könnte beispielsweise lauten: | ||
1. Bringe die Ziffer 1 mit dem Buchstaben | 1. Bringe die Ziffer 1 mit dem Buchstaben i in Übereinstimmung. | ||
2. Dechiffriere sodann die ersten 7 Buchstaben. | 2. Dechiffriere sodann die ersten 7 Buchstaben. | ||
3. Drehe die Scheibe dann um 9 Schritte gegen den Gang der Sonne. | 3. Drehe die Scheibe dann um 9 Schritte gegen den Gang der Sonne. | ||
| Zeile 74: | Zeile 72: | ||
6. und dechiffriere die folgenden 21 Buchstaben. | 6. und dechiffriere die folgenden 21 Buchstaben. | ||
7. .... | 7. .... | ||
8. | 8. Irgendwann - je nach Sicherheitsbedürfnis - wird wieder mit Schritt 2 begonnen. | ||
Der Schwachpunkt dieses Systems liegt darin, dass die Abbildung des Klartextalphabetes auf das Chiffrenalphabet eine Konstante in der Zuordnungssystematik aufweist. Immer dann, wenn im Beispiel der dargestellten Grafik das "E" auf das "s" abgebildet wird, wird das "R" auf ein "v" transferiert. Ein Umstand der zu statistischen Häufungen führen kann und damit das System angreifbar macht. Diesem Umstand könnte man durch austauschbare Innenscheiben (Chiffrenalphabete) begegnen, die unterschiedliche Permutationen der verwendeten Zeichen enthalten. | |||
''Anmerkung: Verfolgen Sie diese Idee konsequent weiter, so führt es zur Konstruktion der Enigma und letztendlich zum Data Encryption Standard (DES), wenn Sie akzeptieren, dass Methoden, die auf Zeichen des Alphpabetes angewandt werden, auch auf Bitmuster anwendbar sind.'' | |||
An dieser Stelle scheint es angebracht, einen weiteren maßgeblichen Parameter der Kryptographie einzuführen, nämlich den Schlüssel. Alberti's Scheibe galt als allgemein bekannte und angewandte Methode, | An dieser Stelle scheint es aber auch angebracht, einen weiteren maßgeblichen Parameter der Kryptographie einzuführen, nämlich den '''Schlüssel'''. Alberti's Scheibe galt als allgemein bekannte und angewandte Methode, das Verschlüsselungs-Instrument war im Handel erhältlich. Dennoch galt die Methode damals als sicher, da die Scheibe ohne Kenntnis der "Dreh- oder Scheibentauschanweisung" (= Schlüssel) schwer zum Erfolg führte. Insbesondere dann nicht, wenn die Anweisung entsprechend komplex war. | ||
Auf die formale Notation wirkt sich die Einführung des Schlüssels folgendermaßen aus: | Auf die formale Notation wirkt sich die '''Einführung des Schlüssels''' folgendermaßen aus: | ||
krypt = CHIFF (key, klar) | krypt = CHIFF (key, klar) | ||
klar = DECHIFF (key, krypt) | klar = DECHIFF (key, krypt) | ||
Den Methoden CHIFF und DECHIFF wird neben dem Klartext bzw. Kryptogramm zusätzlich noch der Schlüssel bereitgestellt. Während die Methode allgemein bekannt | Den Methoden CHIFF und DECHIFF wird neben dem Klartext bzw. Kryptogramm zusätzlich noch der Schlüssel bereitgestellt. Während die Methode allgemein bekannt sein darf, gilt es nur mehr den Schlüssel geheim zu halten. Eine große Errungenschaft, die jedoch noch immer den Nachteil birgt, dass sich unterschiedliche KommunikationspartnerInnen sozusagen bilateral geheime Schlüssel aushandeln müssen. Ein Merkmal jeder symmetrischen Verschlüsselung, welches auch für die Computerkryptographie bis zur Erfindung der asymmetrischen Verfahren galt. | ||
== Enigma == | == Enigma == | ||
Statt Scheiben | Statt Scheiben wurden rotierende Walzen in schreibmaschinen-ähnliche Apparate eingebaut welche durch Elektromotoren angetrieben eine Fülle unterschiedlicher Chiffrenalphabete erzeugen. Jeder Anschlag auf der Tastatur führt automatisch zu einem neuen Alphabet, bis die rotierende Walze wieder an ihren Ausgangspunkt zurückgekehrt ist. | ||
[[Datei:Enigma_rotor.gif ]] | [[Datei:Enigma_rotor.gif ]] | ||
Viele Versionen der 1920 von Arthur Scherbius entwickelten Verschlüsselungsmaschine "Enigma" sind bekannt und wurden auch als "legendäre Enigma" noch während des 2. Weltkrieges eingesetzt. Vorläufer der heutigen "Computer" vermochten - vor allem durch | Viele Versionen der 1920 von Arthur Scherbius entwickelten Verschlüsselungsmaschine "Enigma" sind bekannt und wurden auch als "legendäre Enigma" noch während des 2. Weltkrieges eingesetzt. Vorläufer der heutigen "Computer" vermochten - vor allem durch eine große Anzahl von Versuchen - die durch Enigma chiffrierten Texte dennoch zu knacken. Von da an hat sich die Kryptographie zur [[Computerkryptographie]] gewandelt. | ||
== Literatur == | == Literatur == | ||
| Zeile 103: | Zeile 104: | ||
* Kevin Mitnick, Die Kunst der Täuschung, Heidelberg 2006 | * Kevin Mitnick, Die Kunst der Täuschung, Heidelberg 2006 | ||
== Zitiervorschlag == | |||
''Mittendorfer'' in ''Höller'', Informationsverarbeitung I, Kryptographie#Überschrift (mussswiki.idb.edu/iv1) | |||
Aktuelle Version vom 1. Oktober 2018, 14:09 Uhr
| Die Kryptographie verhalf über Tausende von Jahren hinweg dem Wunsch, Nachrichten nur an die berechtigten (gemeinten) Empfänger geraten zu lassen, zur teilweisen Erfüllung. Die heute vorherrschende Computerkryptographie will noch immer dasselbe und einiges darüber hinaus. |
Chiffren und Codes
Der Begriff "Chiffre" stammt aus dem Arabischen (sifr) und bedeutet soviel wie "nichts". Chiffren waren bereits in der griechischen und römischen Kultur von großer Bedeutung. In der europäischen Kultur wurden Chiffren im Mittelalter von Geheimbünden, weltlichen und kirchlichen Autoritäten benutzt und sind in zahlreichen Formen und Anwendungen bekannt bzw. erhalten.
Während Chiffren mit dem Ersetzen (Substitution) und Vertauschen (Transposition) von Buchstaben und singulären Zeichen arbeiten, verwenden Codes ganze Wörter bzw. Begriffe. Der Einsatz der Chiffren erwies sich jedoch als flexibler und ist im Zusammenhang mit der Anwendung von Computerprogrammen vielseitig anwendbar, sodass die heutige Anwendung der Kryptographie als Weiterentwicklung der Methoden des Chiffrierens angesehen werden kann.
Begriffe
Die unverschlüsselte Botschaft wird allgemein als Klartext, der Vorgang des Verschlüsselns als Chiffrieren und das Ergebnis der Verschlüsselung als Geheimtext oder Kryptogramm bezeichnet. Das Rückführen des Klartextes aus dem Kryptogramm nennt sich Dechiffrieren. Die Verallgemeinerung des Chiffrierens wird als Kryptographie bezeichnet.
In formaler Schreibweise wird das soeben Beschriebene wie folgt dargestellt:
krypt = CHIFF (klar)
klar = DECHIFF (krypt)
Der Klartext "klar" wird mit der Methode "CHIFF" in den Geheimtext "krypt" verwandelt. Der Geheimtext "krypt" wird mit der Methode "DECHIFF" wieder in den Klartext "klar" rückverwandelt.
Der systematische Versuch, den Klartext ohne Kenntnis der Methode und der Schlüssel rückzuverwandeln, heißt Kryptoanalyse.
Das Ziel des Chiffrierens war Jahrhunderte lang dasselbe: Es galt zu verhindern, dass Unberechtigte in Kenntnis von geheimen Botschaften kamen. Heute, im Zeitalter der globalen Vernetzung, sind die Zielsetzungen und Anwendungsgebiete der modernen Kryptographie vielfältiger.
Transposition und Substitution
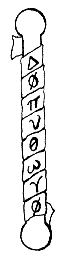
Zwei Methoden beherrschen die Chiffrierung: das Vertauschen der Zeichen des Klartextes, die Transposition, und das Ersetzen des Klartextalphabetes durch ein Chiffrenalphabet, die Substitution. Das Prinzip der Substitution kann als allgemein bekannt angenommen werden, denn es wurden und werden Geheimalphabete bereits in jungen Jahren gerne eingesetzt. Ein einfaches Transpositionsbeispiel findet sich aus vorchristlicher Zeit, die Skytale.
Ein Streifen Leder, Pergament oder Tuch wurde um einen Stab gewickelt. Die geheime Botschaft wird vertikal auf den Streifen geschrieben. Abgewickelt, ergeben die Buchstaben eine sinnlose Reihenfolge. Nur wer das Geheimnis des Wickelns kennt, über den richtigen Stab mit dem richtigen Durchmesser verfügt, kann die Botschaft entziffern.
Die Monoalphabetische Substitution
Wie der Name bereits verrät, benutzt die monoalphabetische Substitution ein einziges Chiffrenalphabet, um die Nachricht zu verschlüsseln. Zahlreiche Beispiele aus der Geschichte sind bekannt.
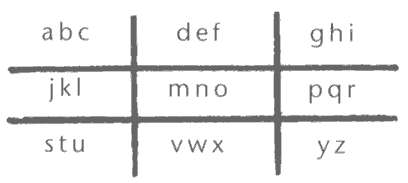
Die Rosenkreuzer-Schablone teilte das Alphabet beispielsweise in neun Felder. Jeder Buchstabe wurde mit den Seitenlinien des entsprechenden Feldes und einem Punkt, der die Position des Buchstabens im Feld symbolisiert, dargestellt.
Die lateinische Bezeichnung für Rosenkreuzer "Rosicrucians", nach der Rosenkreuzer-Schablone chiffriert, ergibt in Anwendung der Rosenkreuzer-Schablone folgende Chiffre:
Neben den Lücken in der Geheimhaltung der Methode ist aus heutiger Sicht die Tatsache, dass die Häufigkeit und die Verteilung der Buchstaben eines Alphabets lebender Sprachen nicht gleichwahrscheinlich ist, größter Schwachpunkt monoalphabetischer Substitution. Die Tatsache der statistischen Häufungen bestimmter (Bit-)Muster wird aber als Positivum in der Datenkompression genutzt.
Mit der Leistungsfähigkeit heutiger Personalcomputer wären die meisten Kryptogramme mit monoalphabetischer Substitution in wenigen Sekunden entschlüsselt.
Polyalphabetische Substitution
Die Tatsache der leichten Knackbarkeit monoalphabetischer Substitution führte bereit im 15. Jahrhundert zur polyalphabetischen Substitution. Dabei wird das Geheimtextalphabet während der Verschlüsselung öfter gewechselt. Je öfter, um so sicherer war und ist die Methode.
Am einfachsten ist die polyalphabetische Substitution anhand der Chiffrierscheibe des italienischen Architekten Leon Battista Alberti darstellbar.
Alberti konstruierte zwei Scheiben, die zueinander verdrehbar sind. Die äußere Scheibe enthält das Klartextalphabet, die innere das Chiffrenalphabet, der Vorgang des Chiffrierens erfolgt durch die Abbildung der Entsprechung von außen nach innen. Die Sicherheit dieser Methode besteht nun darin, dass die Stellung der beiden Scheiben zueinander während der Chiffrierung gewechselt wird. Jede unterschiedliche Stellung der Scheiben zueinander entspricht einem neuen Alphabet. Jede Folge von Stellungswechseln ebenfalls.
Eine Anweisung zum Dechiffrieren könnte beispielsweise lauten:
1. Bringe die Ziffer 1 mit dem Buchstaben i in Übereinstimmung. 2. Dechiffriere sodann die ersten 7 Buchstaben. 3. Drehe die Scheibe dann um 9 Schritte gegen den Gang der Sonne. 4. Fahre fort, 13 Buchstaben zu dechiffrieren. 5. Drehe die Scheibe alsdann 4 Schritte mit dem Gang der Sonne 6. und dechiffriere die folgenden 21 Buchstaben. 7. .... 8. Irgendwann - je nach Sicherheitsbedürfnis - wird wieder mit Schritt 2 begonnen.
Der Schwachpunkt dieses Systems liegt darin, dass die Abbildung des Klartextalphabetes auf das Chiffrenalphabet eine Konstante in der Zuordnungssystematik aufweist. Immer dann, wenn im Beispiel der dargestellten Grafik das "E" auf das "s" abgebildet wird, wird das "R" auf ein "v" transferiert. Ein Umstand der zu statistischen Häufungen führen kann und damit das System angreifbar macht. Diesem Umstand könnte man durch austauschbare Innenscheiben (Chiffrenalphabete) begegnen, die unterschiedliche Permutationen der verwendeten Zeichen enthalten.
Anmerkung: Verfolgen Sie diese Idee konsequent weiter, so führt es zur Konstruktion der Enigma und letztendlich zum Data Encryption Standard (DES), wenn Sie akzeptieren, dass Methoden, die auf Zeichen des Alphpabetes angewandt werden, auch auf Bitmuster anwendbar sind.
An dieser Stelle scheint es aber auch angebracht, einen weiteren maßgeblichen Parameter der Kryptographie einzuführen, nämlich den Schlüssel. Alberti's Scheibe galt als allgemein bekannte und angewandte Methode, das Verschlüsselungs-Instrument war im Handel erhältlich. Dennoch galt die Methode damals als sicher, da die Scheibe ohne Kenntnis der "Dreh- oder Scheibentauschanweisung" (= Schlüssel) schwer zum Erfolg führte. Insbesondere dann nicht, wenn die Anweisung entsprechend komplex war.
Auf die formale Notation wirkt sich die Einführung des Schlüssels folgendermaßen aus:
krypt = CHIFF (key, klar)
klar = DECHIFF (key, krypt)
Den Methoden CHIFF und DECHIFF wird neben dem Klartext bzw. Kryptogramm zusätzlich noch der Schlüssel bereitgestellt. Während die Methode allgemein bekannt sein darf, gilt es nur mehr den Schlüssel geheim zu halten. Eine große Errungenschaft, die jedoch noch immer den Nachteil birgt, dass sich unterschiedliche KommunikationspartnerInnen sozusagen bilateral geheime Schlüssel aushandeln müssen. Ein Merkmal jeder symmetrischen Verschlüsselung, welches auch für die Computerkryptographie bis zur Erfindung der asymmetrischen Verfahren galt.
Enigma
Statt Scheiben wurden rotierende Walzen in schreibmaschinen-ähnliche Apparate eingebaut welche durch Elektromotoren angetrieben eine Fülle unterschiedlicher Chiffrenalphabete erzeugen. Jeder Anschlag auf der Tastatur führt automatisch zu einem neuen Alphabet, bis die rotierende Walze wieder an ihren Ausgangspunkt zurückgekehrt ist.
Viele Versionen der 1920 von Arthur Scherbius entwickelten Verschlüsselungsmaschine "Enigma" sind bekannt und wurden auch als "legendäre Enigma" noch während des 2. Weltkrieges eingesetzt. Vorläufer der heutigen "Computer" vermochten - vor allem durch eine große Anzahl von Versuchen - die durch Enigma chiffrierten Texte dennoch zu knacken. Von da an hat sich die Kryptographie zur Computerkryptographie gewandelt.
Literatur
- F. B. Wrixon, Codes, Chiffren und andere Geheimsprachen, Köln 2000
- Simon Singh, Geheime Botschaften, Die Kunst der Verschlüsselung von der Antike bis in die Zeiten des Internet, München 2001
- Kevin Mitnick, Die Kunst der Täuschung, Heidelberg 2006
Zitiervorschlag
Mittendorfer in Höller, Informationsverarbeitung I, Kryptographie#Überschrift (mussswiki.idb.edu/iv1)